| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- JS
- CSS
- Ajax프레임워크
- R
- 유의수준
- 노트list
- DOMAPI
- 자기지도학습
- 프로토콜
- 웹폰트
- 신뢰구간
- DOM
- 행렬
- 노마쌤과 즐거운 영어 습관
- 클러스터링기법
- Filter
- 매일영어습관
- Ajax
- 벡터
- Mac konlpy
- 파이썬
- 명령어
- 정수인코딩
- HTML
- NLP
- 함수
- 노마쌤
- 인덱스
- EC2
- 질의확장
- Today
- Total
채니의 개발일기
연속형 확률분포(정규분포, 표준정규분포): 정규분포, 지수분포, 표준정규분포, 카이제곱,F분포 본문
연속형 확률분포
- 연속확률변수 : 확률변수 X가 취할 수 있는 값이 무한한 경우 이를 연속확률변수라고 한다 ex)달리기 초, 키
- 이산형 확률분포는 데이터로 분포를 결정지을 수 있는 반면, 연속형 확률분포는 분포를 결정짓지 못한다
- 연속확률분포는 셀 수 없이 많은 확률 변수들의 분포임으로 정확한 값을 표현할수 없다. 따라서 특정구간 a≤x≤b에 대해 확률로 표현한다
- 확률밀도함수(= 확류질량함수 = PDF): 연속확률 변수가 주어진 구간 내에 포함될 확률을 출력하는 함수

- 확률변수 X가 어떤 구간에 속할 확률은 0과1사이
- 확률변수 X가값을 가질수있는 모든 구간의 확률을 합치면 1이다 (전체면적 = 1)
- 𝑓(𝑥) = 확률, 𝑑𝑥= 구간길이
- 확률밀도함수는 a부터 b까지의 구간에 대해 "확률/구간길이"의 값을 모두 더한 값이다.
균등분포
가장 단순한 연속확률분포로, 특정 구간 내 값들이 나타날 가능성이 균등 = 모든 확률변수에 대해 일정한 확률을 가지는 확률분포
X~U(a,b)
X는 a에서b사이에서 일정한 값을 취하고, P(a≤x≤b)=1이다

a=5, b=1 일때, f(x)의 값은?

정규분포
- 정규분포는 평균을 중심으로 분산만큼 퍼진 종 모양의 분포
- 기계학습분야에서 주로 사용
- 분산이 클 수록 양옆으로 넓게 퍼진것을 확인 할 수 있다.
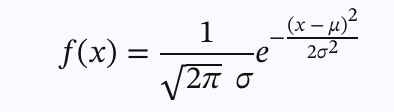
μ는 평균이고 σ는 표준편차
- 확률변수 X의 확률밀도함수가 다음과 같을때, X가 정규분포를 따른다고한다
- 평균μ 와 표준편차 𝜎2에 의해 분포의 모양이 결정된다

A그래프는 분산을 1로 설정
B그래프는 분산을 0.5로 설정
지수분포
특정 시점에서 어떤 사건이 일어날 때까지 걸리는 시간을 측정할때 사용 = 시간에 대한 확률을 구할때
ex) 웹페이지에 평균적으로 10분에 한명씩 방문자가 접속한다. 한명의 방문자가 접속한 뒤에, 그다음 방문자가 올때 까지의 걸리는 시간의 확률은?
- 포아송분포와의 차이점 : 포아송분포 = 발생횟수에 대한 확률, 지수분포 - 대기시간에 대한 확률
지수분포식 : (x≤0일때)
λ: 단위시간 동안 평균 사건 발생횟수
지수분포의 누적 분포함수
- 문제 : 운영중인 서버에는 하루 평균 4건의 해킹이 시도딘다. 첫번재 해킹 시도가 3시간안에 발생할 확률은?

- 지수분포의 특성 : 무기역성
- 특정시점에섭퉈 소요되는 시간은 과거로부터 영향을 받지않는다.
- 한게점 : 현실세계에서 다양한 사례를 모델링하기에는 지나치게 단순한 경향이 있음
표준정규분포
- 정규분포를 따르는 확률변수는 선형조합 역시 정규분포를 따르는 특징이 있음
- 선형조합(linear combination)은 주어진 벡터들을 상수와 함께 선형적으로 결합하는 연산
- 선형조합식: c₁v₁ + c₂v₂ + ... + cₙvₙ (여기서 c₁, c₂, ..., cₙ은 상수(coefficients)이며, v₁, v₂, ..., vₙ은 벡터)
- 선형조합이 정규분포를 따르는 이유는 중심극한정리(Central Limit Theorem)와 연관 있다. 중심극한정리는 독립적인 확률변수들의 합이나 평균이 정규분포에 근사적으로 따른다는 결과를 의미
- 이 성질을 이용해 정규분포를 표준화 할 수 잇음
중심극한정리 관려 포스팅
중심극한정리
중심극한정리 표본크기 (n)가 증가함에 따라, 평균의 표본 분포가 정규 분포에 근사한다는 이론 동일한 확률분포를 가지는 확률변수로부터 추출된 n개의 표본평균은 n이 클수로 정규분포에 가까
xcwaonvy.tistory.com
- 정규분포를 표준화하는 것은 평균을 0, 표준편차를 1로 만드는 과정
표준편차 구하기***
- 원래의 정규분포를 따르는 확률변수 X가 있다고 가정
- X에서 평균(μ)을 뺀 값을 구합니다. 이를 X에서 평균을 제거한 편차(deviation)라고한다
- X에서 평균을 제거한 편차 = X - μ
- 편차를 X의 표준편차(σ)로 나눕니다. 이를 표준화한 편차(standardized deviation)라고 한다
- 표준화한 편차 = (X - μ) / σ
- 표준화 공식
Z = (X - μ)/σ
- 표준 정규 분포는 확률변수 z가 평균이 0이고, 분산이 1인 정규분포를 따르는 상황이다.
- 이때, Z는 표준정규분포를 따른다고 하며, Z~N(0,1)로 표현한다

- 확률 변수 X의 확률밀도 함수는 위와 같이 표현한다
평균이 0이고 분산이 1인 표준 정규분포

- 누적분포함수 : 아래 그래프에서 정규분포의 누적분포 함수를 확인 할 수 있다.

- 정규분포의 누적 분포함수값에 대한 표인 표준정규 분포 표'를 활용한다

카이제곱 분포
분산은 데이터가 평균으로부터 얼마나 퍼져 있는지를 나타내는 지표로 사용
- 분산은 데이터의 변동성을 측정하는데 도움을 주며, 비교 분석에서 결과의 신뢰성을 평가하는 데 중요한 역할을 한다
- 분산을 측정하기 위해서는 제곱합(sum of squares) 구조를 사용
- 제곱합은 각 데이터 값과 평균 간의 차이를 제곱한 값을 합한 것으로, 제곱합을 구하지 않으면 데이터의 중심으로부터 얼마나 떨어져 있는지를 측정할 수 없게 된다
- 분산이 크다는 것은 데이터가 평균에서 멀리 퍼져 있는 것을 의미하며, 분석 결과에 대한 신뢰성을 낮출 수 있다.
- 데이터의 분산을 고려하여 비교 분석을 수행하는 것이 중요합니다.
카이제곱 분포 : 분산의 특징을 나타내는 확률분포
- 카이제곱 분포는 제곱합의 분포
- 주로 적합도 검정(goodness-of-fit test)이나 독립성 검정(independence test) 등에서 사용
- 적합도 검정: 주어진 데이터가 특정 분포와 적합한지를 확인
- 독립성 검정: 두 변수 간의 독립성 여부를 확인하는데 사용
- 카이제곱 분포를 이용하여 검정 통계량을 계산하고, 그 결과를 확률적으로 평가하여 통계적인 결론을 도출할 수 있다
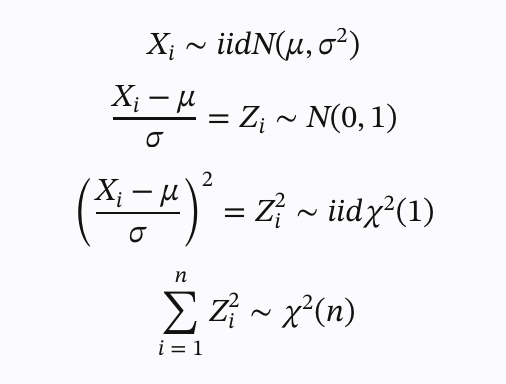
iid: 독립항등분포 = 독립적이고 동일한 분포를 가진다는 의미
정규분포를 따르는 확률변수 Xi에 표준화를 진행해 표준 정규분포 Zi로 변환 -> 자유도가 1인 카이제곱 분포로 변환 ->그 합은 자유도 n인 카이제곱 분포를 따른다는 것을 보여주는 식 : 독립적인 카이제곱 변수들은 가법성으로 인해 서로 더할 경우에도 그 값은 카이제곱 분포를 따름
**자유도란?
통계적 추정을 할 때 해당 분포에서 추정해야 하는 미지수의 개수. = 통계적 추정을 할 때 표본자료 중 모집단에 대한 정보를 주는 독립적인 자료의 수 -> 자유도를 사용하면 표본분산이 모분산에 근사하게 되어 불편추정이 가능합니다. 또한, 자유도를 사용하면 적절한 확률분포를 선택
- 자유도가 3이면 3개의 확률변수를 자유롭게 추정가능
자유도가 5인 카이제곱 분포

F 분포
F 분포는 독립된 두 집단의 분산을 비교하는데 사용되는 확률분포.
F 분포는 두 개의 카이제곱 분포를 나눈 값으로 정의되며, 분자와 분모의 자유도에 따라 분포의 모양이 결정된다
- 두 개의 독립된 집단의 분산을 비교할 때, 카이제곱 비를 계산하여 비교를 진행
- 카이제곱 비는 두 집단의 분산의 비율로, 분자의 분산을 분모의 분산으로 나눈 것.
- 카이제곱 비가 1에 가까울수록 두 집단의 분산이 동일하다고 가정할 수 있다.

-> Q1과 Q2는 각각 자유도가 n1과 n2인 카이제곱 분포를 따르는 확률변수이고, Q2/n2Q1/n1는 자유도가 (n1,n2)인 F 분포따른다
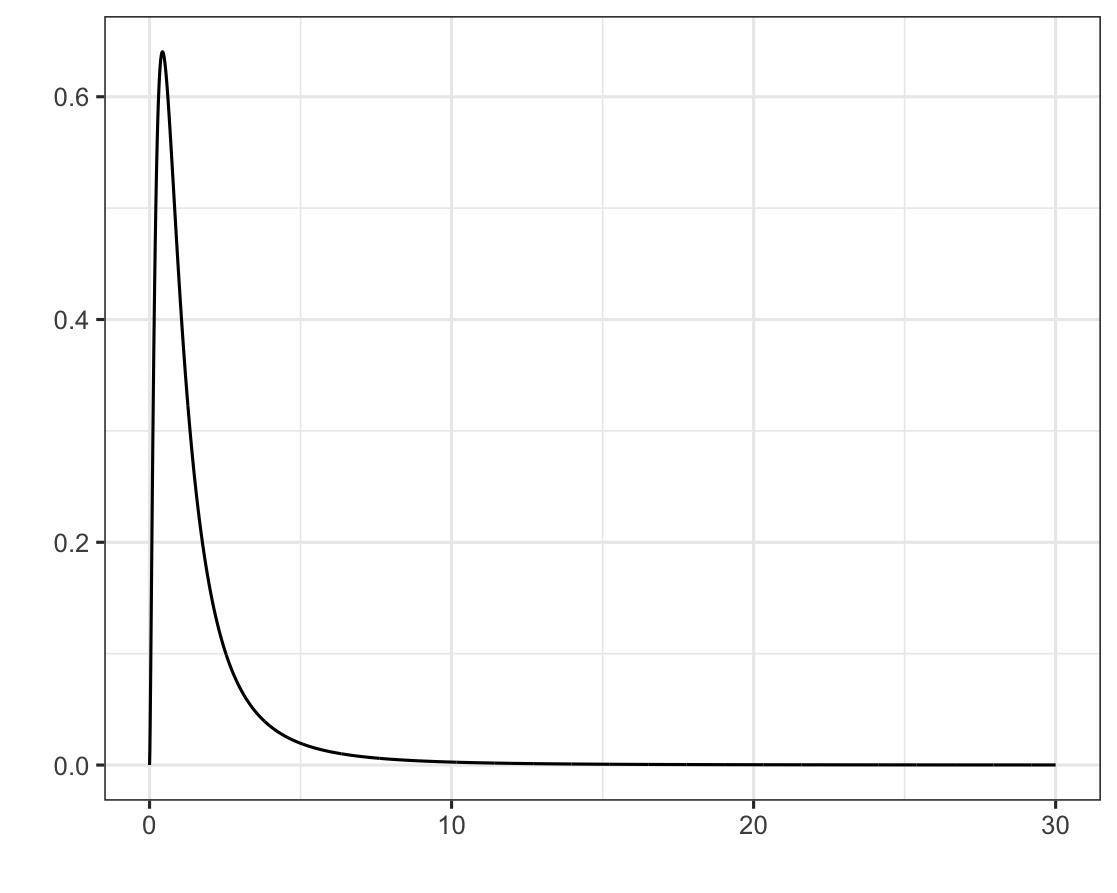
library(ggplot2)
k1 =c()
p1 =c()
for (k in seq(0,30,by=0.01)){
p = df(x=k, df1=5, df2=5)
k1 =c(k1,k)
p1= c(p1,p)
}
ggplot()+
geom_line(aes(x=k1,y=p1))+
theme_bw()+
theme(legend.position = 'none')+
xlab("")+ylab("")
'수학 > 통계학' 카테고리의 다른 글
| 통계적 의사결정 (0) | 2023.07.23 |
|---|---|
| 데이터분포 탐색하기 (분포의 치우침, 왜도,첨도) (0) | 2023.07.23 |
| 중심극한정리 (0) | 2023.07.03 |
| 확률분포, 이산형확률분포(확률질량함수,베르누이시행) (0) | 2023.06.17 |
| 모수와 통계량(기댓값,모평균,표본평균,분산,편차) (0) | 2023.06.08 |




